Piecewise Calibration

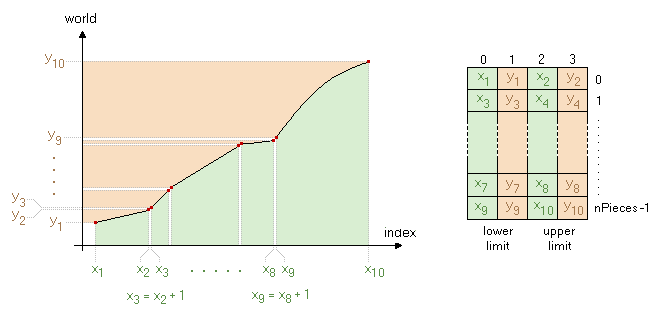
The calibration model of Epina ImageLab is quite flexible. For each axis Epina ImageLab provides one or several calibration functions which map each index of the data array to the corresponding world coordinates. The calibration function can be any kind of polynomial function of orders zero to six, including piecewise calibration functions of different orders.

Technical implementation: the metadata container maintains two individual polynomial functions for each index of the four-dimensional data cube, one function for the forward transform (converting indices to world coordinates) and one for the inverse transform (world coordinates to indices). This elaborate scaling scheme ensures that almost any kind of calibration can be achieved to a high level of precision. Please keep in mind, that the calibration functions may not necessarily differ from index to index, in fact, in many cases the calibration function is constant over all indices of a given axis (i.e. the lateral calibration is normally a linear one with constant parameters, since non-linear calibration will distort the resulting image).

Under practical circumstances the only calibration function which is more complicated than a simple linear relationship will occur along the spectral axis. For example, a data cube might contain three different kinds spectra (= spectral groups) which of course requires at least three different calibration functions. Another example for a more complex calibration function is the piecewise combination of various functions along the spectral axis (as it may occur with instruments containing several detectors).

Please note that calibration functions - even piecewise ones - have to be monotonous with no gaps in between (i.e. there must be a valid forward and inverse function for each index of the axis and the indices of adjacent calibration function must be consecutive at the boundaries). The extended version of Epina ImageLab provides several ILabPascal functions which support the calculation and management of calibration functions, i.e. GetCalibCoeffs, SetCalibCoeffs, RecalcCalibPieces and CalcInvCalibCoeffs.

Hint:

Calculating the inverse of a polynomial functions might pose problems and cannot be solved exactly for all kinds of polynomials (assuming that the maximum order of the polynomials is restricted to six and only positive integer powers are used). You have to assure that the forward and the inverse polynomials do not differ too much (i.e. the difference between the two polynomials should never be greater than the measurement accuracy of your instrument). When developing calibration polynomials you should test this difference over the entire calibration range.